Zadání : Příklad 6 : Napište rovnici kružnice se středem S [ 5 ; -1] , jejíž tečna má rovnici t : 3x + 4y + 14 = 0
Řešení :
Uvedeme dva postupy řešeníA) Pomocí sestavení a řešení kvadratické rovnice kdy D = 0
B) Pomocí normály a určení průsečíku normály a zadané přímky jako dotykového bodu
A)
1)Vyjádříme
y z rovnice přímky2) Napíšeme středový tvar rovnice kružnice a dosadíme souřadnice středu.
3) Nalezneme společný bod kružnice a tečny společným řešením rovnice tečny a rovnice kružnice tím že za
y v rovnici kružnice dosadím y z rovnice přímky tedy :Po sečtení všech zlomků a úpravách
dostaneme kvadratickou rovnici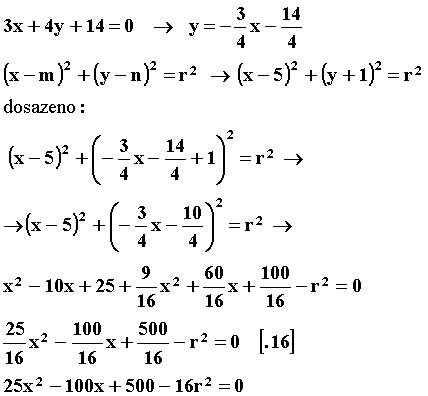
Kvadratická rovnice má ale dvě neznámé
x a r. Nás zajímá poloměr r při kterém se kružnice zadané přímky dotýká. Protože se ale přímka dotýká - má společný jen jeden bod- tedy jedno řešení, musí být diskriminant kvadratické rovnice roven 0. Řešíme rovnici zD = 0 pro r
Pro rovnici kružnice máme všechny údaje
:zadané souřadnice středu S i r
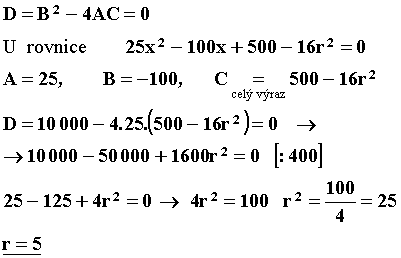
B)
Normála je kolmice k tečně, která prochází středem kružnice. Máme-li rovnici tečny
3x + 4y + 14 = 0 , víme z kapitoly o přímkách, že přímky jsou k sobě kolmé jestliže poměr jejich koeficientů je v tomto vztahu :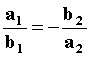
Rovnice normály tedy je ®

Společným řešením rovnice normály a zadané rovnice tečny nalezneme souřadnice dotykového bodu
T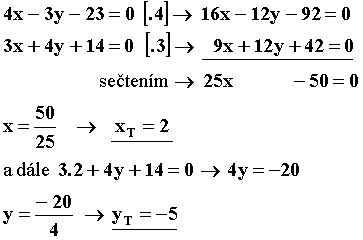
Vzdálenost mezi S a T je poloměr kružnice r. Středová rovnice kružnice je : (x - m)2 + (y - n)2 = r2.
kde m, n jsou souřadnice středu
r je poloměr
Rovnice kružnice tedy je :
(x - 5)2 + (y + 1)2 = 25
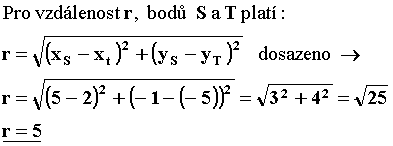
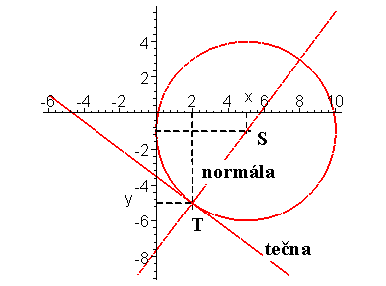
Výsledek : A) B) Rovnice kružnice (středový tvar) je ( x - 5 )2 + ( x + 1 )2 = 25