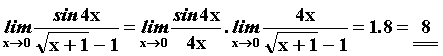Zadání : Vypočítejte :

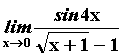
Řešení : Protože přímé dosazení x = 0 vede k neurčitému výrazu musíme limitu upravit. Pro řešení použijeme dvou základních vzorců pro limity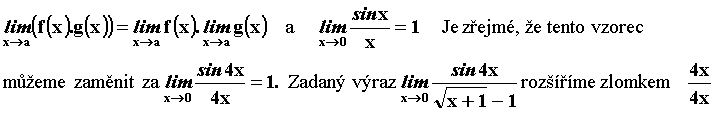

Po rozšíření jsme získali výrazy typu f(x).g(x) (jsou podtržené) a při respektování prvního z uvedených vzorců víme, že limita prvního členu =1. Vypočítáme proto jen limitu druhého členu. Zlomek usměrníme, abychom neměli ve jmenovateli odmocninu a po úpravách, kde se nám vykrátí x obdržíme hodnotu limity druhého členu . A protože limita prvního členu je = 1, je to zároveň výsledek celkové limity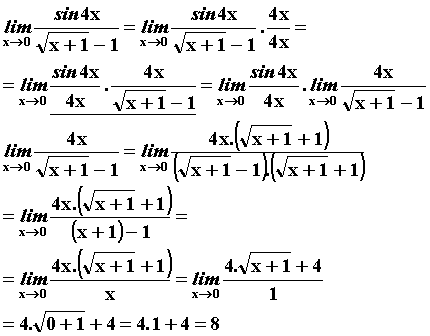

Výsledek :