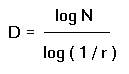FRAKTÁLY, FRAKTÁLOVÁ GEOMETRIE

Matematický obor geometrie, který všichni známe, se zabývá pravidelnými útvary (jako je např. přímka, kružnice, elipsa, n - úhelník,...). Ovšem v reálném světě je většina útvarů nepravidelných. Např. mrak lze aproximovat množinou koulí a elips, ale tím dochází ke značné deformaci a ztrátě informací. Takovými objekty se zabývá fraktální geometrie. Ta popisuje na rozdíl od Euklidovské geometrie objekty ne rovnicí, ale algoritmy, které jsou nejčastěji rekurzivní.
Slovo fraktál poprvé použil B. Mandelbrot pro označení objektů, jejichž tvar je nezávislý na velikosti měřítka, pod kterým objekt pozorujeme. V překladu to znamená "rozlámat na části, vytvořit nepravidelné úlomky". Jako fraktály se tedy označují nepravidelné geometrické útvary rozložitelné na jednotlivé části, z nichž každá je v ideálním případě zmenšenou kopií celku. Mluvíme o tzv. opakování vzoru - soběpodobnosti. Fraktály mívají ještě další zajímavé vlastnosti, např. nekonečně dlouhý obvod nebo naopak nekonečně malý obsah.
Toto samozřejmě není matematická definice fraktálu. Ta zatím ale nebyla přesně ustanovena. Nejvýstižnější je pravděpodobně "definice" již zmiňovaného pana Mandelbrota : Fraktál je možina, jejíž hodnota Hausdorffovy dimenze přesahuje hodnotu dimenze topologické.
Topologická dimenze (DT) určuje klasický geometrický rozměr tělesa. Bod má DT=0, přímka DT=1, plocha DT=2 a prostorový objekt DT=3.
Hausdorffova dimenze D, nebo také dimenze fraktální, určuje míru nepravidelnosti tělesa. U pravidelných těles je shodná s dimenzí topologickou, u těles nepravidelných je větší. Hodnota D u fraktálu, který vznikl n - násobným opakováním je potom :

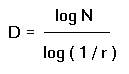kde r ... koeficient měřítka, N ... počet soběpodobných částí

Př: Výpočet D pro jednoduchý fraktál, známý pod názvem vločka Kochové. tato množina vznikne následujícím rekurzivním postupem : vezmeme strany rovnostranného trojúhelníku a vyjmeme z nich prostřední třetinu. Nad vzniklými mezerami sestrojíme vždy dvě strany z rovnostranného trojúhelníku o velikosti stran jedna třetina původní úsečky. V dalším kroku aplikujeme tento postup na všechny úsečky v této množině. Tímto dělením se postupně okraj vločky zjemňuje a po nekonečně mnoha iteracích je její délka nekonečná, přestože ohraničuje konečnou plochu.

Předpokládejme délku strany např.1. po první transformaci se délka změní na 4/3, tedy se zvětšío 1/3.

obr.1

Po každé iteraci vzniknou 4 soběpodobné části (N = 4), délka se zvýší o 1/3 (r = 1/3). Pak

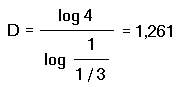
Tato křivka má Hausdorffovu dimenzi 1 < D < 2, je tedy fraktálem. Z prostorových objektů má např. skála dimenzi asi D = 2,2, lidský mozek D = 2,76.

Tento výpočet se ale používá jen pro jednoduvhé fraktály, protože u složitých vzniká problém s určováním konstanty pro závislost délky objektu na velikosti měřítka. v přírodě se často setkáváme s objekty, jejichž tvar nelze přesně popsat pomocí jedné fraktální dimenze - charakterizují se dvěma a více dimenzemi. Těmto objektům se říká multifraktály.

Typy fraktálů podle metod konstruování

Lindenmayerovy systémy (L - systémy)

Klasická konstrukce :

Tyto fraktály vznikají jednoduchými rekurzivnímy postupy, aplikováním rotace, posunutí a změny měřítka bez použitínáhodných čísel. Několik příkladů :

Cantorovo diskontinuum : Z původní úsečky vyjmeme prostřední třetinu a tento proces aplikujeme rekurzivně na zbývající dvě třetiny. Fraktální dimenze D = log 2 / log 3 = 0,63 (je větší nežli dimenze přímky, ale menší než dimenze bodu).

obr.2

Sněhová vločka Kochové : viz dříve

Sierpinského fraktál : je to lineární deterministický fraktál, který vznikne z trojúhelníku rekurzivním vyjímáním trojuhelníku vzniklého spojením středů jeho stran. fraktální dimenze D = log 3 / log 2 = 1,58.

obr.3

Rozvoj této skupiny byl umožněn díky jejich aplikaci na modelování rostlin:

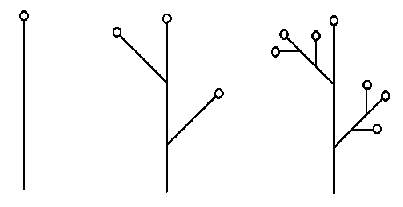obr.4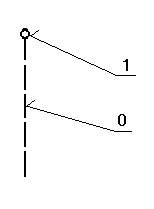obr.5

Existují dva způsoby, jak je popsat :

čísly : viz obr.5

přepisovací gramatikou, která bude využívat následující abecedu :

F ..... pohyb dopředu

+ ..... otočení o úhel alfa doleva

- ..... otočení o úhel alfa doprava

(pro mé příklady jsem použil alfa = PI / 3)

Přepisovací pravidla pro vločku Kochové :

krok 0 : F

krok 1 : F = F + F - - F + F

krok 2 : F = F + F - - F + F + F + F - - F + F - - F + F - - F + F + F + F - - F + F

obr.6

 

 

Pro případ květiny musíme ještě k uvedeným přepisovacím pravidlům přidat další dvě ( čímž umožníme větvení ) :

[ ..... push - ulož na zásobník

] ..... pop - vem ze zásobníku

F = F [ - F ] F [ + F ] F

obr.7

 

Těmito postupy se generují symetrické objekty - jsou vždy stejné. reálné mají různé úhly natočení. Využívá se pravděpodobnosti, např. :

p1 = 0,4, p2 = 0,6

dle těchto pravděpodobností se volí některé z přepisovacích pravidel.

Afinní transformace IFS (iterační funkční systémy)

Tento systém se používá pro generování textur. Hlavní rozdíl spočívá v tom, že každému zobrazení je přiřazena určitá pravděpodobnost, se kterou je aplikováno. Vstupem do algoritmu pak není skupina bodů, ale pouze bod jediný. Tento bod pak náhodně postupně vykresluje celý objekt.

IFS (w, P) : kde w ... transformace, P ... pravděpodobnost, platí že součet pravděpodobností musí být roven jedné.

Sierpinského trojúhelník pomocí IFS : použijí se tři jednoduché transformace počátečního bodu, z nichž každé přidělíme pravděpodobnost p = 1/3 :

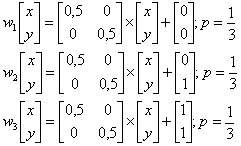obr.8

Několik počátečních iterací a výsledný obrázek (např. po 10000 iteracích) :

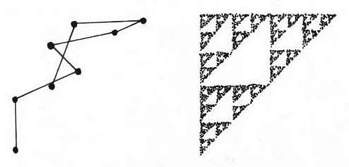obr.9

v případech kdy je možné nalézt vhodná transformační pravidla, lze využít IFS k modelování přírodních struktur :

obr.10

Fraktály v komplexní rovině

Jedná se o nelineární fraktály, jejichž algoritmy postupně vykreslují trajektorii bodů v průběhu iteračního procesu. Dělí se na :

1. trajektorie leží uvnitř určité oblasti

2. Trajektorie směřuje do nekonečna

jde - li tedy trajektorie do nekonečna (opustí kruh daného poloměru), vybarvíme ho jednou barvou. body, jejichž trajektorie směřuje dovnitř vybarvíme druhou barvou. Dojem lze ještě vylepšit barevním rozlišením dle toho, po kolika iteracích opustí trajektorie sledovanou oblast (kruh). např. po 20. iteracích modře, po 50. zelene, po 200. fialově...

matematickým základem pro tvorbu těchto fraktálů jsou iterační rovnice, kde bod bereme jako komplexní číslo. Nejznámější je pak rovnice :

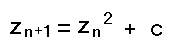
která je základem pro velmi známý fraktál Mandelbrotova množina :

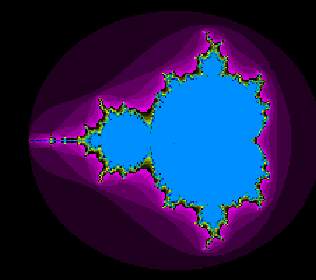obr.11

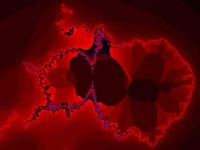
Tento typ fraktálů je na pohled asi vizuálně nejpřitažlivější a proto na závěr pár obrázků :

Závěr

Díky moderním počítačům lze počítat a generovat složité fraktály, které se využívají pro tvorbu textur, obrázků, videa atd. tvůrci nejsou omezeni jen na 2D, ale využívají i prostoru, náhodných faktorů a pravděpodobnosti, čímž se snaží co nejvíce přiblížit realitě.